Educação

Curva de Nível

Integração por Partes

Como Fazer Mínimos Quadrados na Casio- fx-82MS

IV Seminário de Tecnologia e Gestão

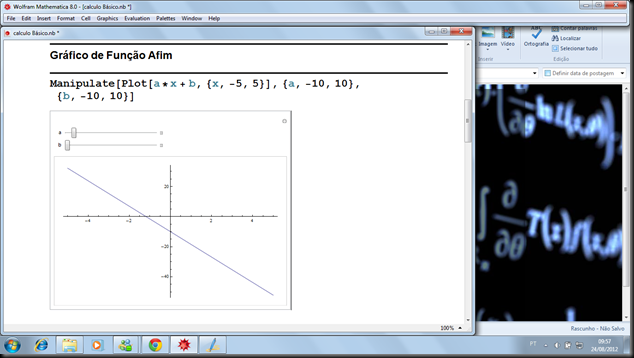
Gráfico de Função Afim : Amanda

 

Utilize este comando e crie manipuladores nos gráficos.

Manipulate[Plot[a*x + b, {x, -5, 5}], {a, -10, 10}, {b, -10, 10}]

Clique nos arquivos e veja mais algumas aplicações:

https://docs.google.com/open?id=0B6V2PAQ5bC4GM0k1MlFoZjI2TDg

https://docs.google.com/open?id=0B6V2PAQ5bC4GYTdDR0ZVNzgwTnM

Contribuição da Aluna Juliana Martinez - Álgebra Linear - Resolução de Sistemas Lineares

è só clicar no link:

http://www.sigecon.com.br/teste/denilson.aspx

Respondendo: Amanda

 

utilize o  PlotRange -> {-10, 10}  para definir os valores do eixo de y, Conforme abaixo:

 

Respondendo

Log[x + 1] é o Ln(x+1) é o logaritmo natural.
e o
Log10[x + 1]  é o log(x+1) na base 10.

grato,

Denilson Paulo

Respondendo

Boa tarde Professor!
> Não estou conseguindo achar erro menor que 5x10^-9 para (exercício 7)
> ln(x+1) com 1<x<10. Consegui erro = -1.37211*10^-9, mas com x=-0.1

Pode deixar este erro mesmo, deixe o email.

Bissecção–intervalo [-1,3 ;–0,8]

 

https://docs.google.com/spreadsheet/pub?key=0AqV2PAQ5bC4GdG50TUhXdXktcFJKX2todWZ4b05KcVE&output=html

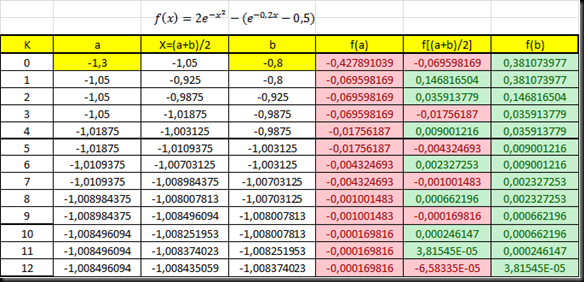
Exercício–Bissecção e Newton Raphson

1 -
Encontre a localização das raízes pelo gráfico,
g(x) = sqrt(x)     raiz de x;

h(x)=5*exp(-x)

Plot[{Sqrt[x], 5 E^-x}, {x, 0, 6}],

Observe que as funções se cruzam entre [1,2], assim aplica o método,

Bissecção:

Newton- Raphson

O critério de parada é f(x)<10^(-2)

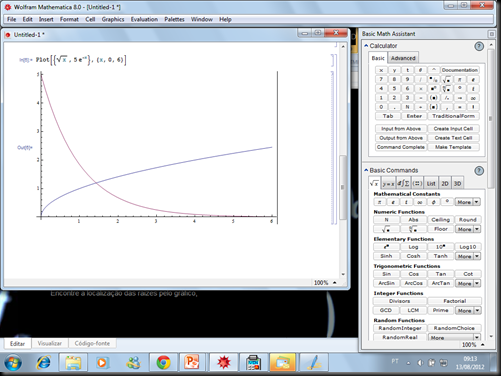
Como Desenhar um Gráfico no Mathemática 8

Para desenhar uma função escreva,

Plot[ f(x), {x, a, b}],

Onde f(x) é a função, a e b, são os valores máximo e mínimo do domínio.

Exemplo:

Plot[Sin[x], {x, -6, 6}],

Se quiser colocar duas funções com o mesmo domínio, é necessário colocá-las entre chaves {},

Plot[{Sin[x], 4*Cos[2*x]}, {x, -6, 6}], 

Qualquer dúvida deixe um comentário.

Mathemática

Baixe a versão de testes,

http://www.wolfram.com/mathematica/trial/

Séries de Taylor

A a série de Taylor é uma série de funções da seguinte forma:



A série de Taylor é uma expansão de uma série de funções ao redor de um ponto.


A constante a é o centro da série que pode ser encarada como uma função real ou complexa.
Se a = 0, a série também é chamada de Série de Maclaurin (de Colin Maclaurin).

Para calcular uma expansão em séries de Taylor no Mathematica utiliza-se:
Series[f(x), {x, a, n}]

Onde:

f(x) é a função ;

a é o ponto;

exemplo:

a) Obtenha a série de McLaurin para a  f(x)= exp(x)

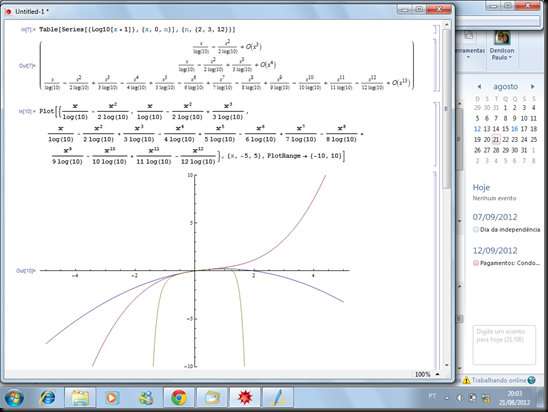
b) Obtenha os polinômios de aproximação para n=2, 3 e 12

c) Considerando o intervalo [-1,1], faça o gráfico das aproximações n=2, 3 e 12;

o Gráfico,

História do Cálculo - Teorema Fundamental do Cálculo

O Teorema Fundamental do Cálculo

        Quando pensamos nas origens geométricas das derivadas e integrais, retas tangentes a curvas e áreas, respectivamente, não existe pista alguma que sugira o Teorema Fundamental do Cálculo. Para Eudoxo (cerca de 370 a.C.), Euclides (cerca de 300 a.C.), Arquimedes (287--212 a.C.), Apolônio (cerca de 262--190 a.C.) e todos os outros matemáticos da antiguidade clássica, retas tangentes, quadraturas e cubaturas não tinham lugar de destaque dentre outros problemas geométricos. Para estes matemáticos, o Teorema Fundamental do Cálculo teria sido uma grande surpresa.
 

    Quando álgebra foi usada pela primeira vez para descrever curvas na geometria analítica de René Descartes (1596--1650) e Pierre Fermat (1601--1665), podemos ver os primeiros lampejos de uma conexão entre tangentes e quadraturas. Em seu estudo das "parábolas de ordem superior", y = kxⁿ, onde k é constante e n = 2, 3, 4, …, Fermat desenvolveu a fórmula y/k para a subtangente em qualquer ponto sobre a curva. A partir daí, e do nosso ponto de vista hoje, teria sido fácil encontrar a fórmula para a derivada; mas para Fermat, nx^n-1 não era o objetivo. Em alguma época na década de 1640, Fermat mostrou que a área entre qualquer uma das parábolas de ordem superior e o eixo horizontal, para 0 £ x £ a, era igual à área do retângulo de largura a e altura aⁿ/(k+ 1). Hoje, podemos ver que Fermat estava torturantemente próximo do Teorema Fundamental do Cálculo, como teria sido expresso em termos de suas parábolas de ordem superior. Mas aquilo não parecia ser de seu interesse.
 

        Fermat também antecipou o Teorema Fundamental do Cálculo no procedimento que desenvolveu para encontrar o centro de gravidade de um conóide (agora conhecido como um parabolóide de revolução), um problema que tinha se originado com Arquimedes. Mas, falhou em reconhecê-lo. Para encontrar o centro de gravidade de um sólido mais geral, Gilles Personne de Roberval (1602--1675) usou um processo somatório e ambas a tangente e a quadratura de certas curvas, mas também não observou a conexão. Gregory St. Vincent (1584--1667) e Evangelista Torricelli (1608--1647) adicionaram à técnica de Roberval para determinar centros de gravidade sem perceber quaisquer outros princípios matemáticos importantes. Em suas notas não publicadas até sua morte, Torricelli desenvolveu sua construção de retas tangentes a "hipérboles de ordem superior" de Fermat, ym = kxn, a partir da quadratura destas curvas, mas sem qualquer pista de idéias mais abrangentes e gerais. Adicionalmente, Torricelli relacionou a construção de retas tangentes a espirais, rm = kq n em coordenadas polares, à quadratura da espiral. Os resultados de Torricelli eram bem conhecidos de seus alunos, principalmente Vincenzo Viviani (1622--1703), e, através dele, James Gregory (1638--1675) e Isaac Barrow (1630--1677) quando este posteriormente viajou e estudou na Itália. Desta maneira, muitas das técnicas do que agora chamamos de cálculo foram transmitidas para a Inglaterra.
 

        De uma maneira indireta envolvendo retificação (para encontrar o comprimento de um segmento de uma curva), James Gregory considerou a área entre a curva, y, e o eixo t, começando em t = a como uma função do extremo direito, t=x. Então encontrou a reta tangente a esta nova curva em t=x e mostrou que sua inclinação neste ponto era igual à ordenada, y, da curva original. Este processo tortuoso aproximou Gregory da Parte 1 do Teorema Fundamental do Cálculo da maneira que é afirmado no livro de Cálculo de Thomas. Mas este resultado era uma pequena parte do livro Universal Part of Geometry (Parte Universal da Geometria,1668) de Gregory, sua tentativa de resumir e organizar a geometria do cálculo como ele a conhecia (o muito da qual tinha aprendido durante seus estudos na Itália, 1664--1668). Ele não só não procurava o Teorema Fundamental do Cálculo aqui, como também não estava usando as fórmulas convenientes usadas hoje em dia.
 

        Isaac Barrow foi o primeiro professor da cadeira Lucasiana de Matemática e Filosofia Natural em Cambridge (1663--1669). Devido às semelhanças em educação e formação de seus escritores, o Geometrical Lectures (1670) de Barrow e o Universal Part of Geometry de Gregory cobriram praticamente o mesmo assunto. O trabalho de Barrow se aprofundou de alguma maneira nos esforços do século 17 levando ao desenvolvimento do cálculo. Em particular, em vários lugares, Barrow mostrou no mínimo uma compreensão intuitiva do fato que tangentes e quadraturas eram operações inversas. Ao discutir velocidade e distância, mostrou como a reta tangente a uma curva (distância) poderia levar à construção e quadratura de outra curva (velocidade), e vice-versa. No seu tratado mais abrangente, Barrow primeiro mostrou geometricamente que a área entre uma curva crescente, mas arbitrária, f(t), e o eixo horizontal, a £ t £ x, era igual a y vezes a subtangente de uma curva auxiliar, h(x), onde y é a ordenada da curva dada em t = x. A linguagem geométrica de Barrow provavelmente escondeu o fato de que seu h(x) era, na realidade, um múltiplo constante do que agora chamamos de antiderivada, F(x).

        Desta maneira, também antecipou a Parte 1 do Teorema Fundamental do Cálculo. Mais além, no seu Geometrical Lectures, Barrow provou um teorema relacionando a soma de retângulos infinitesimais preenchendo a região entre uma curva e o eixo horizontal, a £ x £ b, ao retângulo cuja largura é uma constante e cuja altura é F(b) - F(a) em notação moderna. Esta é a essência da Parte 2 do Teorema Fundamental do Cálculo como encontrado no livro de Cálculo de Thomas. O livro Geometrical Lectures de Barrow foi o ápice dos processos geométricos do século 17 que levaram às nossas modernas derivada e integral. Embora seu aluno e protegido, Isaac Newton (1642--1727), o tenha encorajado a incluir alguns métodos algébricos adicionais no seu trabalho, Barrow era no fundo um geômetra muito talentoso. Assim não percebeu que o cálculo, através do Teorema Fundamental do Cálculo, é uma entidade intelectual única.
 

        Graças aos fundamentos providos por Barrow, Isaac Newton (1642--1727), se aperfeiçoou nos resultados da tangente e quadratura dos primeiros dois terços do século 17. Em uma carta a Gottfried Wilhelm Leibniz (1646--1716), Newton afirmou claramente, em termos físicos, o que os dois problemas mais básicos de cálculo eram (e ainda são): "1. Dado o comprimento do espaço continuamente [isto é, em todo instante de tempo], encontrar a velocidade do movimento [isto é, a derivada] em qualquer tempo dado. 2. Dada a velocidade de movimento continuamente, encontrar o comprimento do espaço [isto é, a integral ou a antiderivada] descrita em qualquer tempo proposto". Mas no lugar de derivadas, Newton empregou flúxions de variáveis, denotados, por exemplo, por x, e em vez de antiderivadas, ele usou o que ele chamou de fluentes.
 

        A partir de Gregory, Newton adotou a idéia que a área entre uma curva, y, e o eixo horizontal, era dependente do extremo direito, t = x. De fato, Newton pensou na área como sendo realmente gerada pelo movimento da reta vertical t = x. Assim o flúxion da área era simplesmente yx. Então, a técnica de Newton para encontrar tais quadraturas era encontrar o fluente de y, equivalente a encontrar nossas antiderivadas; este é o cerne da Parte 2 do Teorema Fundamental do Cálculo como encontrado no livro Cálculo de Thomas. Newton usou o Teorema Fundamental do Cálculo para encontrar os valores exatos para várias áreas, da mesma maneira que fazemos hoje. Em geral, Newton começou a pensar nos problemas geométricos de cálculo em termos algébricos.
 

        Newton resumiu quase todos os trabalhos anteriores sobre cálculo. Juntamente com Barrow, foi especialmente influenciado por La géométrie de René Descartes (1596--1650) numa tradução em Latim e com comentários por Frans van Schooten (1615-1660) e por John Wallis (1616--1703) em seu The Arithmetic of Infinites. Ele coroou seus estudos com sua própria genialidade, escrevendo três manuscritos sobre cálculo: o primeiro foi escrito em outubro de 1666; o segundo em 1669; e o terceiro, atualizando seus dois trabalhos anteriores, em 1671. Em seu trabalho mais famoso, o Principia Mathematica (1687), Newton usou as idéias e algumas das técnicas de cálculo, mas como o Principia foi escrito em sua maior parte na forma geométrica, as fórmulas e partes algébricas do cálculo estavam ausentes. As três monografias de cálculo de Newton, contudo, foram amplamente conhecidas através de cópias feitas para seus colegas da Sociedade Real. Mas elas não foram publicadas até muito depois de sua morte.
 

        Quando Leibniz foi a Paris em 1672 em missão diplomática, foi introduzido a idéias emergentes de cálculo por Christiaan Huygens (1629--1695), um membro da nova Academia Francesa. Leibniz estudou muitos dos trabalhos de autores de matemática avançada, e relatou que aqueles de Blaise Pascal (1623--1662) eram especialmente úteis. A maior parte dos escritos de Leibniz sobre cálculo recaíram em três grupos: seus manuscritos - quase todos diários - começaram enquanto ele estava em Paris (1672--1676); os artigos que publicou no Acta Eruditorum nas décadas de 1680 e 1690; e um manuscrito, History and Origin of the Differential Calculus (História e Origem do Cálculo Diferencial,1714), sobre o qual falaremos a seguir.
 

        As idéias de Leibniz sobre integrais, derivadas e cálculo em geral foram desenvolvidas a partir de analogias com somas e diferenças. Por exemplo, para o Teorema Fundamental do Cálculo, se fosse dada uma seqüência finita de números tais como, Y: 0, 1, 8, 27, 64, 125, e 216, com diferenças y: 1, 7, 19, 37, 61, e 89, ele notou que a soma das diferenças, å y = (1 - 0) + (8 - 1) + (27 - 8) + … + (216 - 125) se alternavam em torno da diferença entre o primeiro e o último valor de Y, 216 - 0. Agora, para Leibniz, uma curva era um polígono feito de um número infinito de lados, cada um com comprimento "infinitesimal". Então, escreveu em 1680, "Eu represento a área de uma figura pela soma [infinita] de todos os retângulos limitados pelas ordenadas e diferenças das abscissas", isto é, como ò ydx. Então, "elevando a alturas maiores" se baseando na analogia com somas finitas e diferenças, Leibniz afirmou que ao encontrar a área representada por ò ydx, deve-se encontrar uma curva Y tal que as ordenadas y são diferenças de Y, ou y = dY. Em termos modernos, Y é nossa antiderivada, e assim, Leibniz formulou uma afirmação inicial da Parte 1 do Teorema Fundamental do Cálculo como encontrado no livro Cálculo de Thomas. Posteriormente, em um artigo de 1693 no Acta Eruditorum, Leibniz escreveu, "o problema geral de quadraturas pode ser reduzido a encontrar uma curva que tenha uma dada lei de tangência", e continuou a especificar esta lei na forma da Parte 2 do Teorema Fundamental do Cálculo.
 

        Para apreciar completamente as contribuições de Leibniz ao cálculo, devemos considerar seu contexto dentro do seu significativo trabalho em lógica, metafísica e filosofia porque pensava em todas estas atividades como inter-relacionadas. Para Leibniz, a existência de infinitésimos poderia ter sido um problema filosófico interessante, mas não observou o ponto em seu cálculo. Cálculo, especialmente o teorema Fundamental, "continha uma maneira prática de computar" e era uma abreviação dos métodos rigorosos das tangentes e quadraturas de Arquimedes (287--212 a.C.) e outros geômetras gregos clássicos. Por outro lado, Jakob (1654--1705) e Johann Bernoulli (1667--1748) e outros matemáticos e cientistas do século 18 que se aproveitaram do cálculo de Leibniz, especialmente de sua notação fértil, usaram livremente, expandiram e aplicaram o cálculo, freqüentemente com resultados espetaculares.
 

        Infelizmente, em torno da virada do século 18, alguns poucos seguidores de Newton atacaram Leibniz acusando-o de plágio do cálculo de Newton durante suas visitas a Londres em 1673 e 1676. Newton e Leibniz nunca se encontraram frente a frente, mas durante as primeiras décadas do século 18, Newton era presidente da Sociedade Real e Leibniz ainda era um membro. Leibniz escreveu seu History and Origin of the Differential Calculus (1714) para sua defesa, mas sem sucesso. A matéria se tornou uma disputa prioritária de escala monumental e se tornou um descrédito para todos os participantes à medida que o século 18 avançou; por exemplo, numa lealdade mal direcionada, a maior parte dos matemáticos ingleses se limitaram aos flúxions e fluentes de Newton e evitaram as notações superiores de Leibniz até o início do século 19. O consenso hoje, depois de muito estudo meticuloso e imparcial, feito por vários estudiosos, é que Newton e Leibniz desenvolveram o Teorema Fundamental do Cálculo independentemente e que, portanto, deveriam dividir igualmente a glória da criação do cálculo.
 

        Leibniz argumentou sobre o Teorema Fundamental do Cálculo por analogia e Newton baseou sua justificativa em flúxions e fluentes, que por sua vez dependiam da intuição de pontos se movendo ao longo de uma curva. Colin Maclaurin (1698--1746) provou a Parte 1 do Teorema Fundamental do Cálculo para funções de potência simples, y = xⁿ, onde n = 1, 2, 3, …, e Joseph Louis Lagrange (1736--1813) estendeu a idéia básica de Maclaurin a funções crescentes representadas por uma série de potências. A prova moderna do Teorema Fundamental do Cálculo foi formulada para funções contínuas em a £ x £ b por Augustin Louis Cauchy (1789--1857) em seu Lessons Given at the École Royale Polytechnique on the Infinitesimal Calculus (1823). Os argumentos que Cauchy deu são os mesmos daqueles encontrados no livro de Cálculo de Thomas, Finney, Weir & Giordano. Com seu Teorema Fundamental do Cálculo, Cauchy proveu a chave, para todas as funções contínuas, que finalmente uniu rigorosamente os dois ramos principais do cálculo em uma estrutura, ambos elegantes e úteis.

Fonte: Geraldo l. Diniz

Transformada de Laplace

Transformada inversa de Laplace

Cálculo de Integral - Passo-a-Passo

Escreva a função que deseja integrar.

Desenhar Gráficos em 3D de funções.

Escreva a função que deseja desenhar o gráfico e os limítrofes do gráfico, isto é, os valores do eixo das abscissas (x), ordenadas (y) e cotas (z).

Se tiver alguma dúvida, deixe nos comentários responderei.

Calculadora de Integrais

Séries de Fourier no Mathemática - Exemplo

Séries de Fourier no Mathemática

Séries de Fourier

A função do Mathemática:


FourierTrigSeries[F,t,n]

onde:
F - função desejada
t - variável independente
n - número de termos da série

exemplo:

>> FourierTrigSeries[t^2+3,t,10]

resulta em:

Agora, se vc quiser plotar o gráfico,

Mas, se pretende plotar todos os 10 termos da expansão, utilize o seguinte comando table (tabela):
onde:

a: numero de termos
F: função
Plot : desenhar o gráfico {t, intervalo incial, intervalo final}
% - desenhar o que está no prompt;
se tirar o ; do table aparecerá uma tabela com todas as 10 expansões.

Experimente desenhar 1 a 1.

Se quiser fazer download do Mathemática:
https://www.wolfram.com/mathematica/trial/

Se quiser o DVD gratuitamente (versão 30 dias)
https://www.wolfram.com/mathematica/contact-us/